Post by The Librarian on May 22, 2008 19:34:52 GMT -7
Tenishna - The Dimensional Stack (Incomplete)
--------------------------------------------------------------------------------
Keep in mind that dimensional theory is just that: theory. These are concepts to be interpreted differently and with a critical eye. Many ideas about the dimensions are wholly improvable and unobservable and thus are created by means of deduction, inference, and imagination. The nature of the dimensions detailed below are drawn from common theory. There are multiple popular dimensional theories and what's elaborated here is a rather simple mixture of them especially manipulated for use in the RP world. All hypothetical application or manipulation of the dimensions is purely imaginative and conceptual.
--------------------------------------------------------------------------------
The basics of the dimensions:
The basics of dimensions are not a very difficult concept to understand. If you were given a dimensional model to look at it would require little time or effort to understand how all the dimensions worked together (see Rob Bryanton's Ten Dimension theory for a layman’s explanation of one theory), however you'll find that different theories have different ideas about just how exactly the dimensions function and their relationship to each other.
These first four dimensions you will find are virtually universally as the same amongst all dimensional theories. I’m not going to spend a lot of time on the first three as they should be rather intuitive.
Zeroth Dimension:
I'm going to start with the zeroth dimension as being a point. We're going to define a point in the mathematical sense, so that a point is dimensionless and only represents location. You can graphically represent the zeroth dimension as a point.

First Dimension:
Assuming we're using length, width, and depth to describe the first three dimensions, the first dimension would be one of only length without width or depth. An object in the first dimension could be represented by drawing a line between two points.
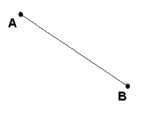
Second Dimension:
A two dimensional object is one with length and width, but with no depth. An easy example is a square, four points connected at perpendicular angles. The second dimension is composed of both the zeroth and first dimension. A membrane when spoken about in conceptual physics can be a two dimensional surface. (For some spectacular reading on the second dimension (and then some) I recommend “Flatland: A Romance of Many Dimensions” by Edwin A. Abbot.)

Third Dimension:
A third dimensional object is one with length, width, and depth. An easy example is a cube, eight points, twelve lines, and six surfaces. Again, an object in the third dimension is composed of the elements of the zeroth, first, and second dimensions. There are no restraints on spatial directional movement in the third dimension. (c.f. Light speed barrier.)
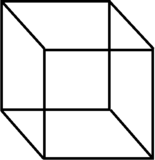
Fourth Dimension:
The fourth dimension is affectionately referred to as time. In our stack of dimensions this is the first one that is not directional or spatial, but rather is represented by movement on a different ‘plane’, in the sense that we can not see it or freely move about in it, but are instead inexorably driven forwards through it. (“Caught up in the river of time.”) Unlike the first, second, or third dimension, movement in the fourth is generally perceived as at a fixed rate and is one directional (disregarding, for the moment, relativity*).
For example: A cube (understandably three dimensional) inhabits a point in the fourth dimension, point X. Somewhere also in the fourth dimension there is a point Y. A point in the fourth dimension will work the way a point in space does; it represents location but occupies no real volume of existence itself, including time. As the cube exists in the fourth dimension it travels from point X to point Y. The travel between these two points is represented by duration, or time. (For example it takes five minutes to travel from point X to Y.) You and I can observe the fourth dimension and that objects in the fourth dimension possess qualities of either first, second, or third dimensional objects.
The fourth dimension can also be visualized by a tesseract, hypercube, or Schlegel diagram.
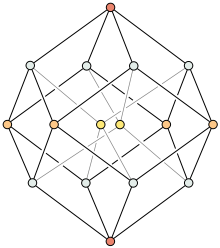
en.wikipedia.org/wiki/Image:8-cell-simple.gif
dogfeathers.com/java/hyprcube.html
As we illustrate the dimensions, the number of vertices doubles with each as we go up. The zeroth dimension, a point, has one, the first dimension, a line segment, has 2 vertices, the second dimension, a square, has four vertices, the third dimension, a cube, has 8 vertices, and the fourth dimension, a tesseract, has 16 vertices. (Visualizations of further dimensions become increasingly complex, which will be brought up later.)
*Regarding relativity, the fourth dimension comes into some trouble when we think of it as moving at a fixed rate. When an object (we’ll say that it is three dimensional, but this would work for any physical thing) is moving extremely fast and pressing the speed of light, relativity perverts the semblance of time between it and other objects. So with respect to the principle of relativity we need to take into very careful consideration how we are measuring the speed and time of three (two or one) dimensional objects traveling through the fourth dimension when we say that they move at a fixed rate. (I’m not going to discuss relativity here, though in another post I’ll elaborate on it so that you can reference it there. This is just a reminder to keep speed and duration in their place.)
After the fourth, the dimensions become far more abstract and theoretical and are predicted entirely from mathematics and theory crafting. Those after the fourth are not by our present senses directly observable.
The Fifth Dimension:
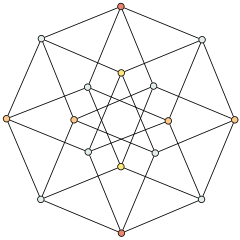
We’ve seen what the dimensions can be visualized as up to the fourth. Introducing the fifth dimension we suppose that the number of vertices moves for 16 to 32, following the doubling standard, to produce a graphical representation called a penteract:
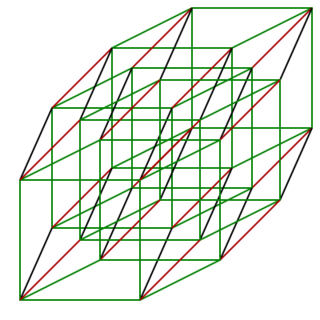

Speculation about the nature of the fifth dimension is broad. I’ll put forwards a few here and allow you to discuss that which you like in more detail as you choose.
The fifth dimension can be taken to be one of probability (which should, as a word, be taken lightly here, for the realm of probability is complex). The idea of the fifth relating to probability ties into alternate reality theories. The fifth would be the place where multiple (really, infinite) numbers of fourth dimension ‘paths’ (which we can say are the timelines that we observe as we move through time) represent any number of existences. For example, you are doing some action right now, namely reading this text. In some alternate reality of fourth, third, second, first, and zeroth dimensions there is a you who is doing something different based on the idea that you, at some point in the past, made a probabilistic decision (an idea based rather solidly on Bayesian theory interpretation) to do something which altered your entire future. So, instead of reading this text, this alternate reality you is instead playing soccer, or something. This would be represented in the fifth dimension.
In an interpretation like Rob Bryanton’s Ten Dimensional theory, the fourth is seen as another point (this point representing the third, second, first, and zeroth dimensions at a particular moment) moving along a line (duration) to another point (the lower order dimensions at another particular moment). The fifth dimension in this model would be a split on this path, where one fourth dimensional point ended up in two different spots at the same moment. This branching out adds another axis which creates the need for the elevation of dimension. This is essentially the same idea as the probability outlook.
A similar idea is proposed in Six Dimensional theory which is based off of Ouspensky’s ideas.* Ouspensky used the analogy of a Frisbee being thrown in a line (the Frisbee being the third dimension, the path of the Frisbee being the fourth, duration). Ouspensky considered the fourth dimension the first dimension of time, and compared it to the first spatial dimension, where the line of the fourth branching out at a right angle created another dimension of time, the fifth. His famous comparison follows that if you were to superposition the Frisbee (render all possible paths of the Frisbee at once), you have the fifth dimension, an outlook which nicely correlates to quantum theory.
Kaluza** studied Einstein’s equations on general relativity, but applied them within the fifth dimension and discovered that the equations Maxwell set up for electromagnetism naturally arose. In the fifth dimension calculations the field equations for gravity and light can be united. (At the time that Kaluza suggested his theory the scientific community was too busy investigating a quantum world which neglected the idea that fundamental forces can be explained by higher-order dimensions and his idea was resurrected by string theorists.) Kaluza suggested that the ether of existence outside of the Big Bang (a sea of quantum information) existed as timeless and as all possible states of all possible particles simultaneously; this is the fifth dimension of which we are but part of, perhaps a mere cross-section.
Another way to expand observation upwards to gain knowledge of higher dimensions falls under the holographic principle (really used to first note the fifth, but applicable higher up). The idea follows that if you bend a one dimensional line, you develop the second dimension. If you bend the second dimensional structure, you develop the third, and so on and so fourth. If you bend the fourth dimension of time you can derive the fifth. Bryanton proposes that the warps and bends in space-time caused by mass (gravity) work as the bend which is needed in the fourth to reveal the fifth. This bend in the fabric Bryanton claims allows us to observe quantum wavestates and allows for superposition.
*Peter Ouspensky was a philosopher and mathematician, not a physicist, but was heavily interested and involved in exploration of higher-order dimensions. He died in 1947, so his theories predate most modern dimensional ideas and in particular string theory, yet still find some truth and relevance. I encourage research about him.
**Theodor Kaluza was a mathematician and a physicist who is notable for developing field equations in five-dimensional space which many believe prove that we live in five dimensions. He died in 1954, again before much modern dimensional theory was popularized, but he laid critical framework for the concept of ‘superposition’ in time and ideas about the nature of the universe. I encourage research about him.
Sixth Dimension:
Ouspensky in his Six Dimension theory puts the six dimension as the extension of the fifth which simply incorporates ‘all possibilities’. Whereas the fifth is simply a superpositioned third dimensional object, only being able to determine itself as one thing in the fourth dimension, the sixth dimension is like a superpositioned superposition. The superpositioned third dimensional object has an infinite number of renderings and paths, but again each can only have one fourth dimension manifestation at the end of each path and rendering. The sixth dimension would be the total sum of all these infinite paths as they repeat infinitely in the duration of the fourth (as the fifth itself is timeless).
(Note: Text is still incomplete.)
--------------------------------------------------------------------------------
Keep in mind that dimensional theory is just that: theory. These are concepts to be interpreted differently and with a critical eye. Many ideas about the dimensions are wholly improvable and unobservable and thus are created by means of deduction, inference, and imagination. The nature of the dimensions detailed below are drawn from common theory. There are multiple popular dimensional theories and what's elaborated here is a rather simple mixture of them especially manipulated for use in the RP world. All hypothetical application or manipulation of the dimensions is purely imaginative and conceptual.
--------------------------------------------------------------------------------
The basics of the dimensions:
The basics of dimensions are not a very difficult concept to understand. If you were given a dimensional model to look at it would require little time or effort to understand how all the dimensions worked together (see Rob Bryanton's Ten Dimension theory for a layman’s explanation of one theory), however you'll find that different theories have different ideas about just how exactly the dimensions function and their relationship to each other.
These first four dimensions you will find are virtually universally as the same amongst all dimensional theories. I’m not going to spend a lot of time on the first three as they should be rather intuitive.
Zeroth Dimension:
I'm going to start with the zeroth dimension as being a point. We're going to define a point in the mathematical sense, so that a point is dimensionless and only represents location. You can graphically represent the zeroth dimension as a point.

First Dimension:
Assuming we're using length, width, and depth to describe the first three dimensions, the first dimension would be one of only length without width or depth. An object in the first dimension could be represented by drawing a line between two points.

Second Dimension:
A two dimensional object is one with length and width, but with no depth. An easy example is a square, four points connected at perpendicular angles. The second dimension is composed of both the zeroth and first dimension. A membrane when spoken about in conceptual physics can be a two dimensional surface. (For some spectacular reading on the second dimension (and then some) I recommend “Flatland: A Romance of Many Dimensions” by Edwin A. Abbot.)

Third Dimension:
A third dimensional object is one with length, width, and depth. An easy example is a cube, eight points, twelve lines, and six surfaces. Again, an object in the third dimension is composed of the elements of the zeroth, first, and second dimensions. There are no restraints on spatial directional movement in the third dimension. (c.f. Light speed barrier.)

Fourth Dimension:
The fourth dimension is affectionately referred to as time. In our stack of dimensions this is the first one that is not directional or spatial, but rather is represented by movement on a different ‘plane’, in the sense that we can not see it or freely move about in it, but are instead inexorably driven forwards through it. (“Caught up in the river of time.”) Unlike the first, second, or third dimension, movement in the fourth is generally perceived as at a fixed rate and is one directional (disregarding, for the moment, relativity*).
For example: A cube (understandably three dimensional) inhabits a point in the fourth dimension, point X. Somewhere also in the fourth dimension there is a point Y. A point in the fourth dimension will work the way a point in space does; it represents location but occupies no real volume of existence itself, including time. As the cube exists in the fourth dimension it travels from point X to point Y. The travel between these two points is represented by duration, or time. (For example it takes five minutes to travel from point X to Y.) You and I can observe the fourth dimension and that objects in the fourth dimension possess qualities of either first, second, or third dimensional objects.
The fourth dimension can also be visualized by a tesseract, hypercube, or Schlegel diagram.


en.wikipedia.org/wiki/Image:8-cell-simple.gif
dogfeathers.com/java/hyprcube.html
As we illustrate the dimensions, the number of vertices doubles with each as we go up. The zeroth dimension, a point, has one, the first dimension, a line segment, has 2 vertices, the second dimension, a square, has four vertices, the third dimension, a cube, has 8 vertices, and the fourth dimension, a tesseract, has 16 vertices. (Visualizations of further dimensions become increasingly complex, which will be brought up later.)
*Regarding relativity, the fourth dimension comes into some trouble when we think of it as moving at a fixed rate. When an object (we’ll say that it is three dimensional, but this would work for any physical thing) is moving extremely fast and pressing the speed of light, relativity perverts the semblance of time between it and other objects. So with respect to the principle of relativity we need to take into very careful consideration how we are measuring the speed and time of three (two or one) dimensional objects traveling through the fourth dimension when we say that they move at a fixed rate. (I’m not going to discuss relativity here, though in another post I’ll elaborate on it so that you can reference it there. This is just a reminder to keep speed and duration in their place.)
After the fourth, the dimensions become far more abstract and theoretical and are predicted entirely from mathematics and theory crafting. Those after the fourth are not by our present senses directly observable.
The Fifth Dimension:
We’ve seen what the dimensions can be visualized as up to the fourth. Introducing the fifth dimension we suppose that the number of vertices moves for 16 to 32, following the doubling standard, to produce a graphical representation called a penteract:


Speculation about the nature of the fifth dimension is broad. I’ll put forwards a few here and allow you to discuss that which you like in more detail as you choose.
The fifth dimension can be taken to be one of probability (which should, as a word, be taken lightly here, for the realm of probability is complex). The idea of the fifth relating to probability ties into alternate reality theories. The fifth would be the place where multiple (really, infinite) numbers of fourth dimension ‘paths’ (which we can say are the timelines that we observe as we move through time) represent any number of existences. For example, you are doing some action right now, namely reading this text. In some alternate reality of fourth, third, second, first, and zeroth dimensions there is a you who is doing something different based on the idea that you, at some point in the past, made a probabilistic decision (an idea based rather solidly on Bayesian theory interpretation) to do something which altered your entire future. So, instead of reading this text, this alternate reality you is instead playing soccer, or something. This would be represented in the fifth dimension.
In an interpretation like Rob Bryanton’s Ten Dimensional theory, the fourth is seen as another point (this point representing the third, second, first, and zeroth dimensions at a particular moment) moving along a line (duration) to another point (the lower order dimensions at another particular moment). The fifth dimension in this model would be a split on this path, where one fourth dimensional point ended up in two different spots at the same moment. This branching out adds another axis which creates the need for the elevation of dimension. This is essentially the same idea as the probability outlook.
A similar idea is proposed in Six Dimensional theory which is based off of Ouspensky’s ideas.* Ouspensky used the analogy of a Frisbee being thrown in a line (the Frisbee being the third dimension, the path of the Frisbee being the fourth, duration). Ouspensky considered the fourth dimension the first dimension of time, and compared it to the first spatial dimension, where the line of the fourth branching out at a right angle created another dimension of time, the fifth. His famous comparison follows that if you were to superposition the Frisbee (render all possible paths of the Frisbee at once), you have the fifth dimension, an outlook which nicely correlates to quantum theory.
Kaluza** studied Einstein’s equations on general relativity, but applied them within the fifth dimension and discovered that the equations Maxwell set up for electromagnetism naturally arose. In the fifth dimension calculations the field equations for gravity and light can be united. (At the time that Kaluza suggested his theory the scientific community was too busy investigating a quantum world which neglected the idea that fundamental forces can be explained by higher-order dimensions and his idea was resurrected by string theorists.) Kaluza suggested that the ether of existence outside of the Big Bang (a sea of quantum information) existed as timeless and as all possible states of all possible particles simultaneously; this is the fifth dimension of which we are but part of, perhaps a mere cross-section.
Another way to expand observation upwards to gain knowledge of higher dimensions falls under the holographic principle (really used to first note the fifth, but applicable higher up). The idea follows that if you bend a one dimensional line, you develop the second dimension. If you bend the second dimensional structure, you develop the third, and so on and so fourth. If you bend the fourth dimension of time you can derive the fifth. Bryanton proposes that the warps and bends in space-time caused by mass (gravity) work as the bend which is needed in the fourth to reveal the fifth. This bend in the fabric Bryanton claims allows us to observe quantum wavestates and allows for superposition.
*Peter Ouspensky was a philosopher and mathematician, not a physicist, but was heavily interested and involved in exploration of higher-order dimensions. He died in 1947, so his theories predate most modern dimensional ideas and in particular string theory, yet still find some truth and relevance. I encourage research about him.
**Theodor Kaluza was a mathematician and a physicist who is notable for developing field equations in five-dimensional space which many believe prove that we live in five dimensions. He died in 1954, again before much modern dimensional theory was popularized, but he laid critical framework for the concept of ‘superposition’ in time and ideas about the nature of the universe. I encourage research about him.
Sixth Dimension:
Ouspensky in his Six Dimension theory puts the six dimension as the extension of the fifth which simply incorporates ‘all possibilities’. Whereas the fifth is simply a superpositioned third dimensional object, only being able to determine itself as one thing in the fourth dimension, the sixth dimension is like a superpositioned superposition. The superpositioned third dimensional object has an infinite number of renderings and paths, but again each can only have one fourth dimension manifestation at the end of each path and rendering. The sixth dimension would be the total sum of all these infinite paths as they repeat infinitely in the duration of the fourth (as the fifth itself is timeless).
(Note: Text is still incomplete.)


